Information Flow and Control Over Networks
Information-based causality measure in a dynamical system:
Information flow and causality are the most fundamental concepts for analyzing and designing various engineering and natural sciences systems.
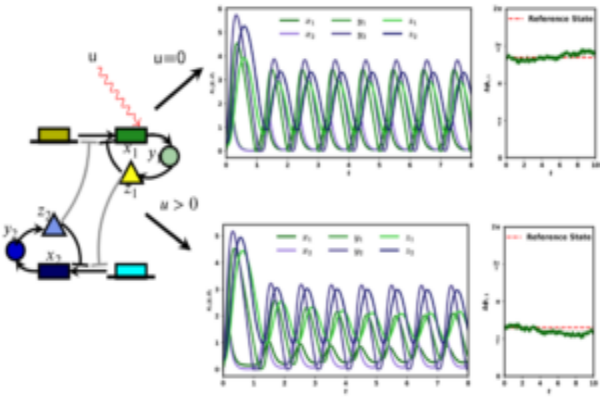
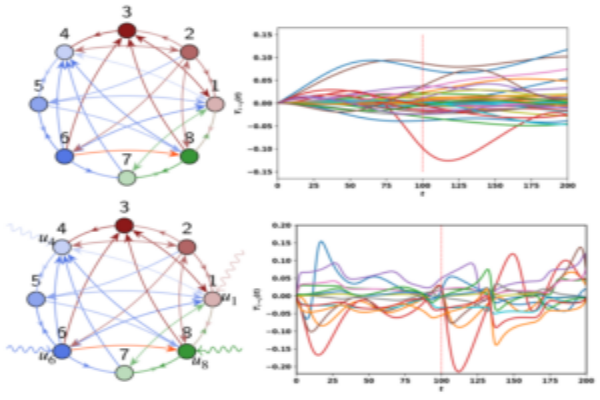
A mathematically precise definition of information flow developed with dynamics in mind is necessary for the rigorous formulation of autonomy in a network dynamical system. The degree of interaction,
as measured by the information flow between a network of autonomous agents and its environment, can be used to characterize the degree of autonomy in a network dynamical system. We have developed novel
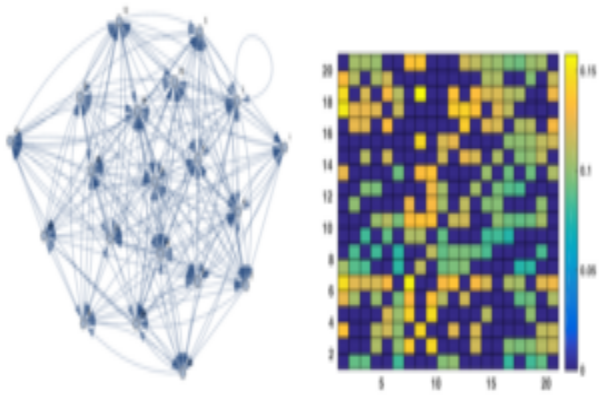
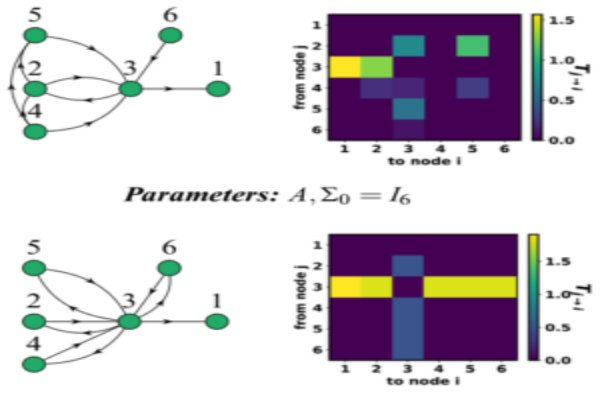
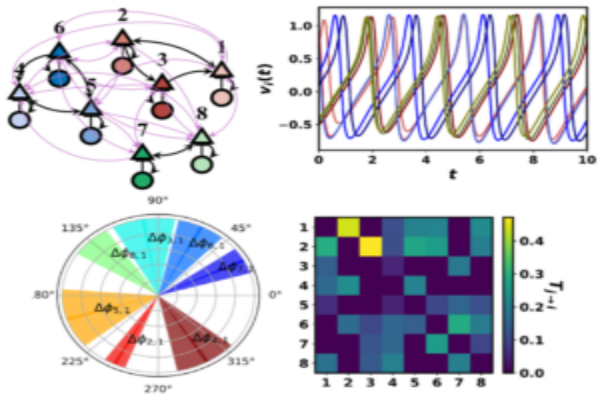
axiom-based formalism for information flow in network dynamical systems using ergodic theory and stochastic dynamics methods.
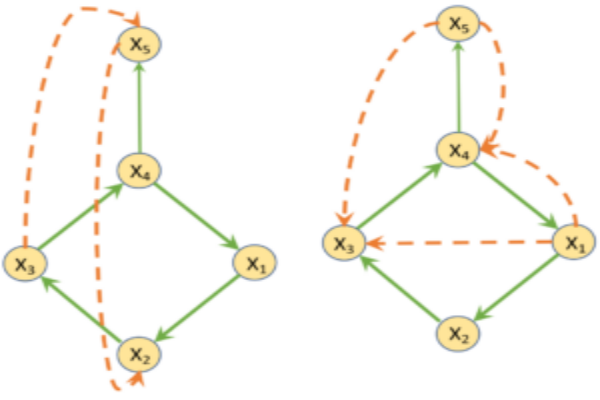
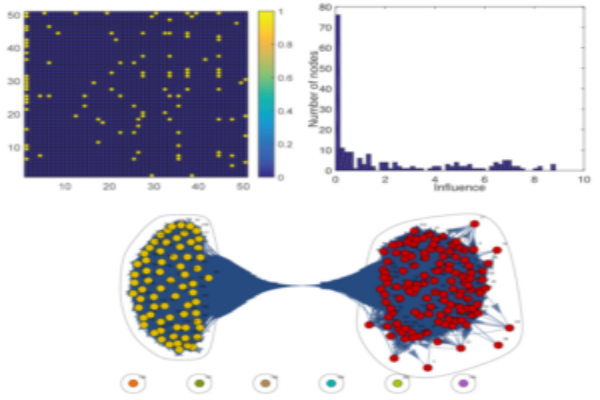
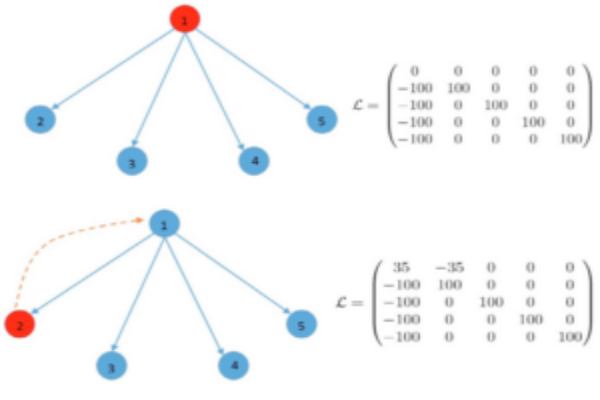
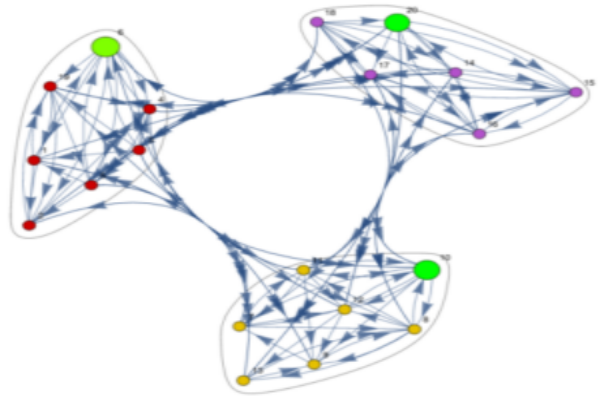
The proposed formalism can be viewed as a natural extension of directed information from information theory to the dynamical system and is used to precisely characterize the flow of information and influence structure in a network dynamical system. The problem of distributed control and estimation in large-scale dynamical network systems is intimately connected with the flow of information among network components. We are investigating the application of information transfer for reduced-order modeling of dynamical systems and for inferring causal structures from brain data.