Research Details

Operator Theoretic Methods for Data-Driven Analysis and Control of Dynamical Systems

Duality in stability and control from linear operator perspective:

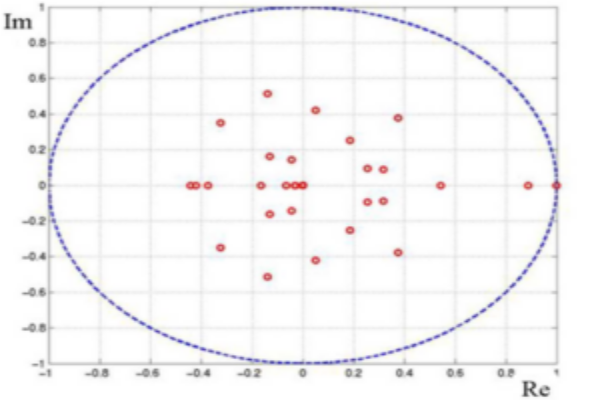
We have introduced novel operator theoretical methods for stability analysis and optimal control design for dynamical systems. The transformative idea we proposed is to shift the focus from the point-wise nonlinear evolution of dynamical systems on the finite-dimensional state space to ensemble linear evolution of functions on infinite dimensional space. With every nonlinear dynamical system, one can associate two linear operators called Perron-Frobenius (P-F) and Koopman operators.

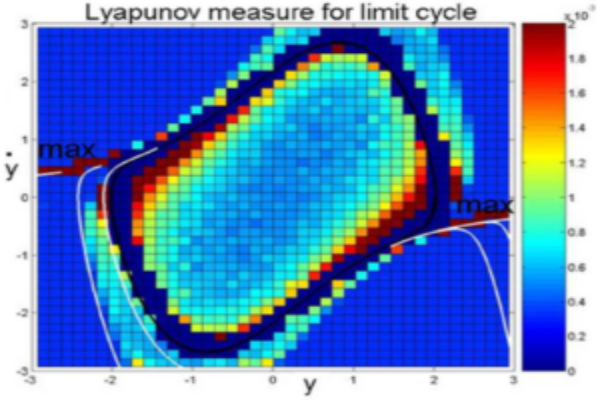
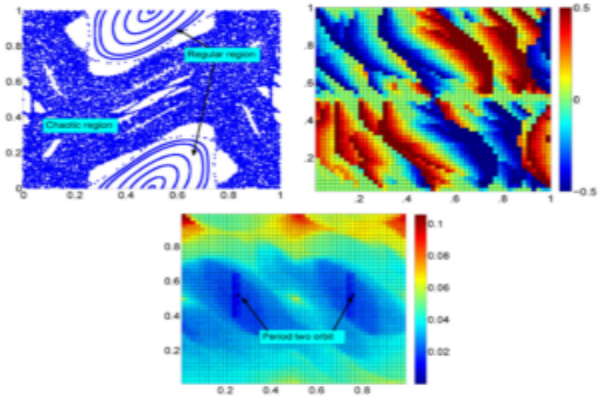
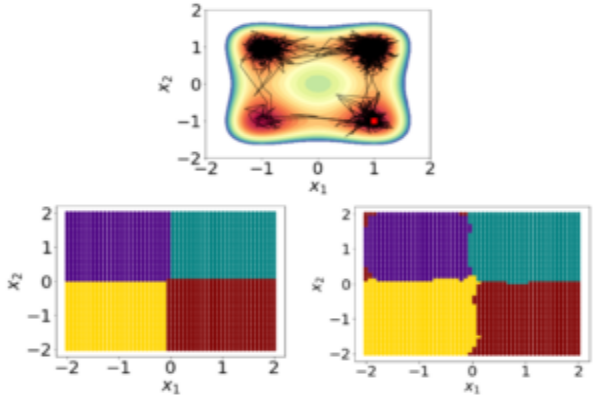
Both these operators provide for the linear description of nonlinear dynamics in the space of densities. This linear description of nonlinear dynamics can be effectively used to analyze and control a nonlinear system.n particular, using a linear transfer P-F operator, we introduce the Lyapunov measure as a new tool for verifying weaker set-theoretic notions of almost everywhere stability. The Lyapunov measure is shown to be dual to the Lyapunov function. Unlike the Lyapunov function, systematic linear programming-based computational methods are proposed to compute the Lyapunov measure.

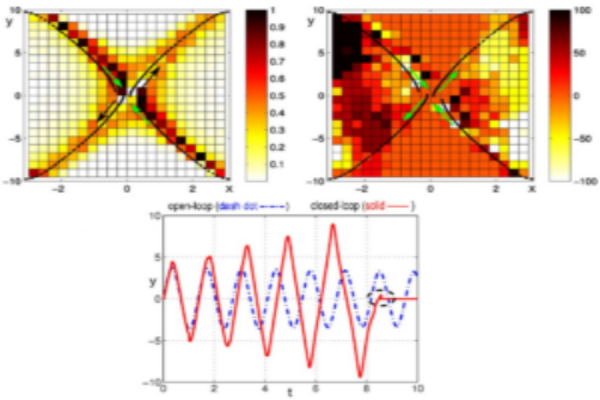
This duality in stability theory between the Lyapunov function and the Lyapunov measure also extends to the optimal control of deterministic and stochastic systems. This duality leads to a convex formulation of optimal control problems in the dual space of densities. These duality results, combined with the data-driven methods discovered for the finite-dimensional approximation of linear operators, are employed to design data-driven optimal control of nonlinear systems. This proposed research aims to find a comprehensive analytical and computational framework for the data-driven control of a dynamical system that explicitly accounts for the finite amount of data available for control.

Spectral Koopman methods for analysis and control:

The proposed research aims to discover methods based on the spectral analysis of the Koopman operator for the data-driven analysis and synthesis of nonlinear systems. The Koopman operator provides for a linear lifting of the nonlinear system dynamics in the function space. The eigenfunctions of the Koopman operator also carry information about the underlying state space geometry. In particular, the stable and unstable manifolds of the nonlinear system can be obtained as zero-level curves of the Koopman eigenfunctions. This connection between the Koopman eigenfunctions and the state space geometry is exploited to analyze and synthesize nonlinear control systems. In our current research, we are developing spectral Koopman methods for reachability analysis, safe control design, uncertainty propagation, and optimal control design. We have established a connection between the eigenfunctions of the Koopman operator and the solution of the Hamilton Jacobi equation.

This connection allows one to approximate the solution of the Hamilton-Jacobi equation using the Koopman eigenfunctions. The approximation of the Koopman operator and its spectrum can be computed from the data without knowing system dynamics. Hence, using Koopman theory provides a natural pathway for developing systematic data-driven analysis and synthesis methods for nonlinear control systems. In our current research, we are exploiting various approaches, including Deep-Neural-Networks, Reproducing Kernel Hilbert Space (RKHS), and techniques inspired by statistical mechanics for approximation of the Koopman spectrum.

Selected Publications

U. Vaidya and P. G. Mehta, Lyapunov measure for almost everywhere stability, IEEE Transactions on Automatic Control, Vol 53, pp. 307-323, 2008.
U. Vaidya, P. G. Mehta and U. Shanbhag, Nonlinear stabilization via control Lyapunov measure, IEEE Transactions on Automatic Control, Vol 55, pp. 1314-1328, 2010.
A. Raghunathan and U. Vaidya, Optimal stabilization using Lyapunov measures, IEEE Transactions on Automatic Control, 2014.
U. Vaidya, Stochastic stability analysis of the discrete-time system using Lyapunov measure, American Control Conference, 2015.
B. Huang and U. Vaidya, Data-driven feedback stabilization using Koopman operator, Book Chapter: Koopman Operator for Control, 2019.
R. Rajaram, U. Vaidya, M. Fardad, and B. Ganapathaysubramanian, Almost Everywhere stability: Linear transfer operator approach, Journal of Mathematical analysis and applications, Vol 368, pp. 144-156, 2010.
B. Huang and U. Vaidya, Convex Approach to data-driven optimal control via Perron-Frobenius and Koopman operator, IEEE Transactions on Automatic Control, 2022.
U Vaidya, D Tellez-Castro, Data-Driven Stochastic Optimal Control With Safety Constraints Using Linear Transfer Operators, IEEE Transactions on Automatic Control 69 (4), 2100-2115.

Operator Theoretic Methods for Data-Driven Analysis and Control of Dynamical Systems

Duality in stability and control from linear operator perspective:

Spectral Koopman methods for analysis and control:

Selected Publications

Contacts

Stay Connected