Research Details

Cyber-Physical Systems

Fundamental limitations for control of dynamical systems over networks:

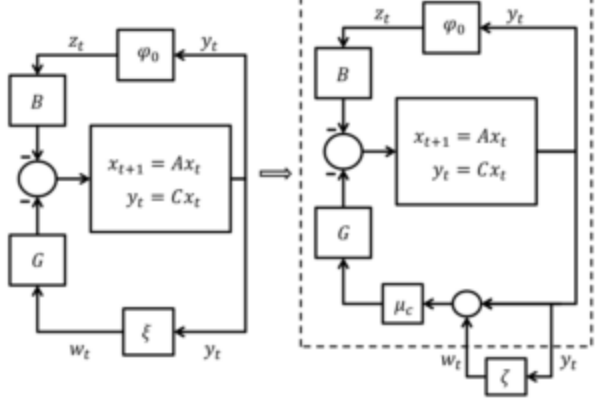
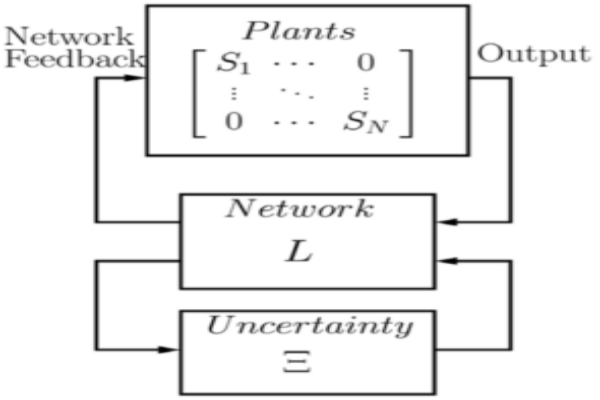
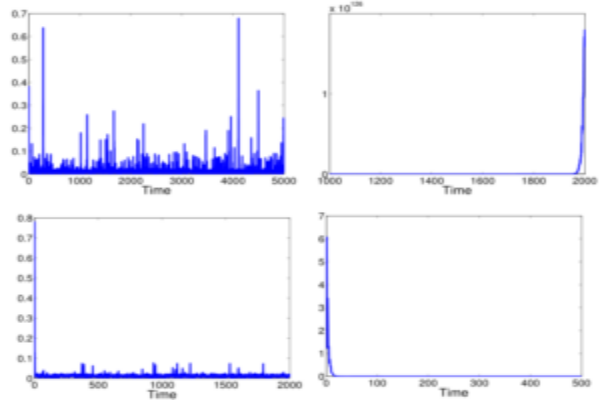
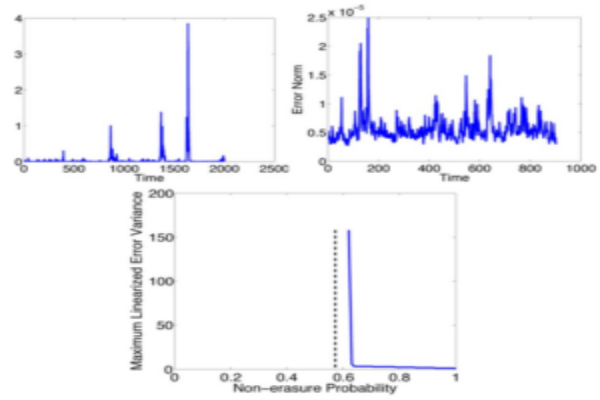
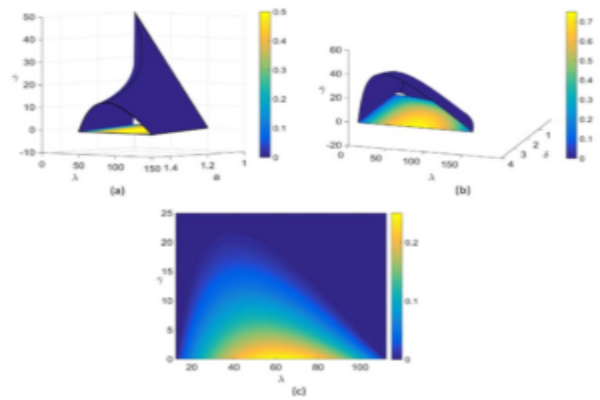
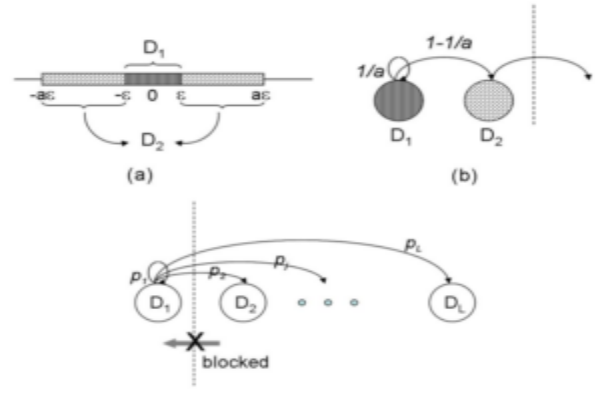
We have discovered a systematic framework for analyzing and designing network-controlled systems in the presence of uncertainty. This includes discovering fundamental limitation results for estimating and stabilizing nonlinear systems over uncertain communication channels. This research mainly connected fundamental limitations for nonlinear stabilization and estimation with the measure-theoretic entropy of steady-state invariant measure of the open loop system. The positive Lyapunov exponents capture the measure-theoretic entropy for a system with non-equilibrium open loop dynamics such as chaotic attractors or unstable limit cycles.

Control and optimization over uncertainty networks:

The main contribution of this work is to understand fundamental tradeoffs that arise in the control of linear and nonlinear dynamical systems over networks in the presence of uncertainty. For systems with linear dynamics, we have provided a systematic convex optimization-based approach for synthesizing control robust to stochastic network communication uncertainty. For systems with nonlinear dynamics, our results offer tradeoffs that arise between the internal dynamics at the individual nodes of the network, network topology, and the communication uncertainty for robust synchronization over the network. Network dynamical systems are also of interest for solving optimization problems in a distributed manner. The dynamical system viewpoint is employed to solve an optimization problem for distributed optimization over the network.Our main contributions to this topic include providing a dynamical systems approach for solving robust optimization problems and finite-time convergence proof for solving time-varying optimization problems.